We present a blueprint algorithm which is an extension to the Greenfield algorithm. The Greenfield algorithm identifies distribution center locations based on customer demand locations where all center locations are unknown at the beginning. However, supplier may want to answer which new distribution locations are required in addition to the existing centers due to increasing customer demand. The Blueprint algorithm identifies new distribution center locations with the existing locations.

Greenfield, Brownfield, and Bluefield

Greenfield analysis is performed to be able to design a new network with all new locations (see the Greenfield analysis). For example, supplier is entering a new market and wants to identify where to locate distribution centers to meet the customer demand. We also talk about Brownfield analysis when network structure stays the same and relations in the network change. For example, supplier may want to keep the current locations but reallocate customers to depots. Bluefield analysis is described as a combination of both brownfield and greenfield, where some part of the network is being built new and some stays the same.

The analysis answers the following questions:

• Where should the new distribution centers be located by keeping the existing locations to minimize cost?
• Which customers will be supplied from each existing and new distribution centers?

Problem

We consider the customer locations in the Greenfield analysis. Demand for each customer is satisfied by a distribution center. Supplier has three existing distribution centers and evaluates to add new centers to satisfy customer demand with minimum cost.

Figure 1 shows the customer locations, corresponding annual demand, and the existing distribution center locations.

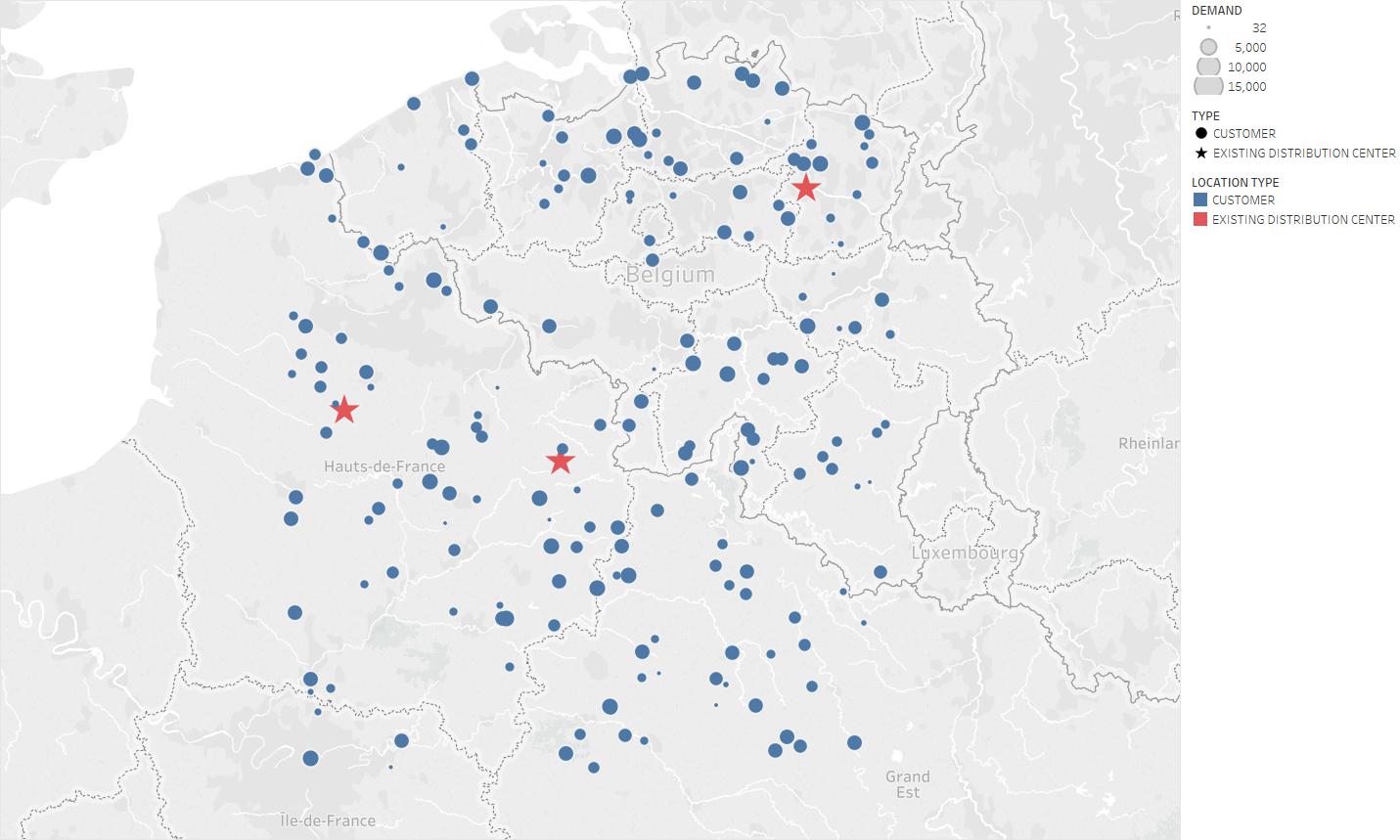Figure 1: Customer demand map with three existing distribution centers

We answer the following questions as a result of the analysis:

• How many new distribution centers are required?
• Where should each new distribution center be located?
• How customers should be allocated to the existing and new distribution centers?

Algorithm

Similar to the Greenfield algorithm, algorithm the new distribution center locations while keeping the existing centers such that total weighted distance to customers is minimized. The following summarizes the algorithm steps.

For given $K_1$ existing and $K_2$ new distribution centers such that $K = K_1 + K_2$ with the corresponding minimum and maximum number of customers and the maximum distance covered by a center,

Step 0: Randomly assign customers to $K$ clusters as each cluster center is a distribution center location. For each customer, calculate the distance to each cluster center using Haversine distance formula. We define the total weighted distance as a summation of customer demand multiplied by distance to each cluster center. Then, set the total weighted distance as previous objective.

Step 1: Run a binary allocation model to allocate customers to $K$ centers.

Step 2: Set total weighted distance as current distance.

Step 3: If current distance is greater than previous distance, then stop. Otherwise, recalculate $K_2$ new center locations as average latitude and longitude of assigned customers to each new center and repeat Steps 1-2 until there exists no better solution with the smallest total weighted distance.

Note that this algorithm is a generalized version of the Greenfield algorithm.

If $K_1=$ and $K_2>0$, then algorithm solves the greenfield problem. If $K_1>$ and $K_2=0$, then algorithm solves the brownfield problem.

Haversine Formula

The Haversine formula calculates the shortest distance between two points on a sphere using their latitudes and longitudes measured along the surface. You can find more detailed explan

Allocation of Customers to Distribution Centers

Similar allocation model in the Greenfield algorithm is used to allocate customers to distribution centers with given cluster locations.

We define model parameters and variables as follows.

Let $C$ be the set of customers and $D$ be the set of distribution centers. Let $d_j$ be total demand for the customer $j\in C$. Let $a_{ij}$ be the distance from the center $i \in D$ to customer $j \in C$. Let $\alpha_i$ be the maximum distance covered by the center $i \in D$. Let $u^{-}_i$ be the minimum number of customers can be allocated to center $i \in D$. Let $u^{+}_i$ be the maximum number of customers can be allocated to center $i \in D$.K

Let $y_{ij}$ be the binary variable for assigning center $i \in D$ to customer $j \in C$.

The following is the binary program for allocating customers to distribution centers.

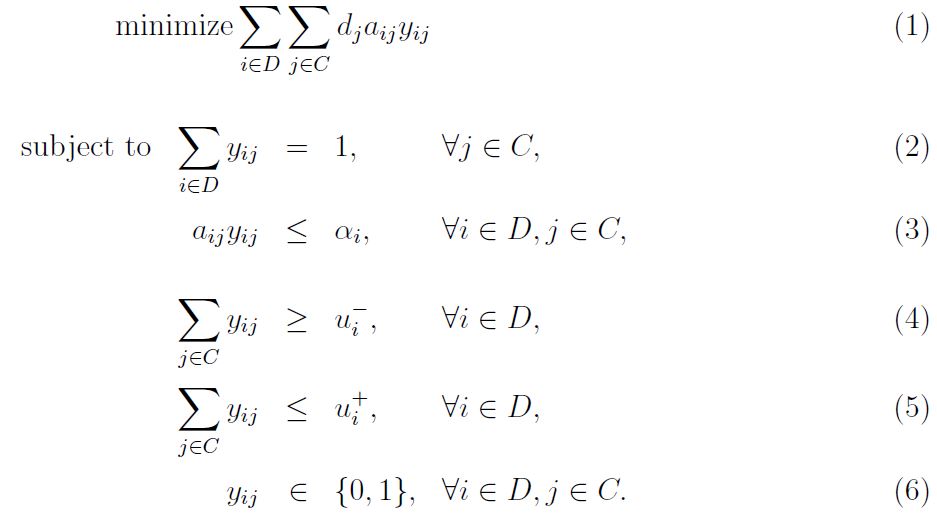
The objective of the model $(1)$ minimizes the total weighted distance. Constraint $(2)$ ensures that each customer is allocated to a center. There exists a maximum distance can be covered by each center $(3)$. Each center has minimum and maximum number of allocated customers as in $(4)$ and $(5)$, respectively. Center to customer allocation is binaries as in $(6)$.

Implementation

The algorithm is implemented in Python. Google OR Tools is used to solve the allocation problem.

You can find the source code at the Bluefield With_Weighted_Kmeans repository on GitHub.

Application

The algorithm is applied on the given problem. We iterate the algorithm for $K=3,\dots,19$. Figure 2 shows run results.

Greenfield and Brownfield Applications