Solving Single Depot Capacitated Vehicle Routing Problem Using Column Generation with Python
Vehicle routing problem (VRP) is identifying the optimal set of routes for a set of vehicles to travel in order to deliver to a given set of customers. When vehicles have limited carrying capacity and customers have time windows within which the deliveries must be made, problem becomes capacitated vehicle routing problem with time windows (CVRPTW). In this post, we will discuss how to tackle CVRPTW to get a fast and robust solution using column generation.

Problem
We consider a pizza restaurant chain, PPizza, in the Los Angeles, CA area with 34 stores. Each store operates from 10am to 1am everyday. PPizza offers three pizza sizes (small, medium, large) with various toppings and soft drinks. Pizzas are prepared with fresh ingredients and baked in store on demand.
PPizza forecasts weekly demand of food items for each store and identifies required ingredients and soft drinks. Fresh ingredients are delivered to stores daily from the main depot once a day. Soft drinks are delivered and replenished by suppliers directly.
Figure 1 shows location of stores and the depot. Each store has time windows between 9am and 3pm where delivery needs to be done within. Unloading time varies by store depending on location and parking availability.
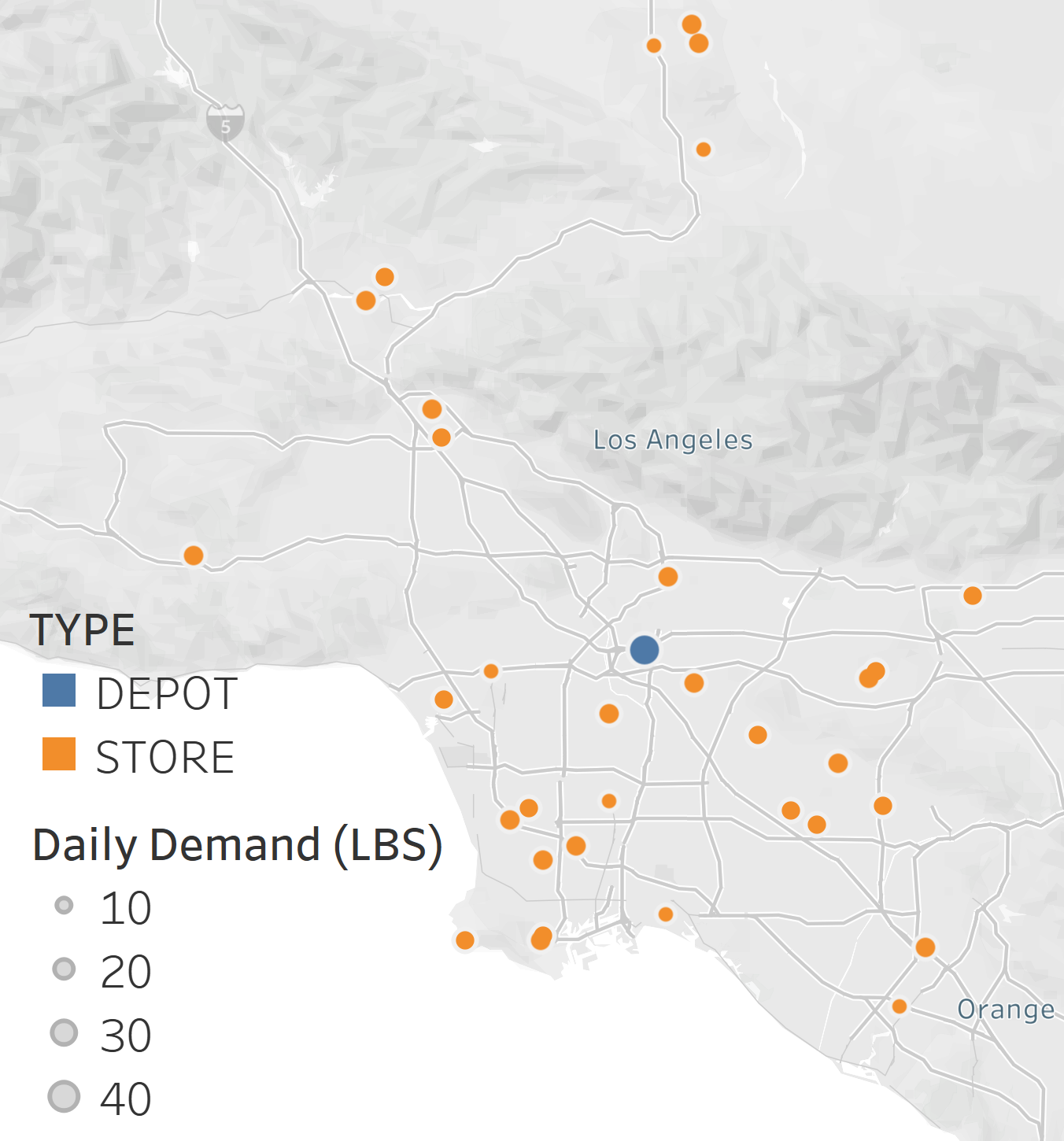 |
|---|
| Figure 1: PPizza depot and stores |
Trucks can leave from the depot at 6am and need to return the depot by 5pm. Each truck can be used once and has a limited capacity of lbs.
Since delivery cost is a function of number of trucks used in delivery, minimizing the total number of trucks used for delivery minimizes total cost. We want to identify the truck operating schedules to be able to deliver fresh ingredients to each store with given time windows by minimizing the total cost (minimizing the number of trucks used).
Analysis
We first formulate the problem as a mixed integer program. Then, we solve the problem for a range of number of available trucks using the formulation. Since CVRPTW is NP-hard, we expect that model run time increases as number of available trucks decreases.
We also develop column generation based algorithm to solve the problem.
Finally, we compare performance of two solution methodologies; mixed integer program and column generation.
General Formulation
We develop a mixed integer model for the PPizza delivery problem as follows.
We solve the mixed integer model using Python with PuLp. The following is the implementation.
import pandas as pd
import timeit
import time
from threading import Thread, currentThread
import queue
from cvrptw_optimization import single_depot_general_model_pulp as sm
# Read input data
customers = pd.read_pickle(r'data/customers.pkl')
depots = pd.read_pickle(r'data/depots.pkl')
transportation_matrix= pd.read_pickle(r'data/transportation_matrix.pkl')
vehicles = pd.read_pickle(r'data/vehicles.pkl')
# Model parameters
bigm_input=transportation_matrix.DRIVE_MINUTES.max()*20
solver_time_limit_minutes_input = 480
# Calculate range for vehicles
min_vehicles = int(round(customers.DEMAND.sum()/60)+2)
max_vehicles = len(vehicles)+1
# Define functions
def run_single_depot_general_model(vehicle,
depots,
customers,
transportation_matrix,
vehicles,
bigm_input,
solver_time_limit_minutes_input):
"""
Run general model
"""
start = timeit.default_timer()
vehicles_sub = vehicles.head(int(vehicle))
print(len(vehicles_sub))
solution_objective, solution_paths = sm.run_single_depot_general_model(depots,
customers,
transportation_matrix,
vehicles_sub,
bigm=bigm_input,
solver_time_limit_minutes=solver_time_limit_minutes_input)
solution_paths['OBJECTIVE'] = solution_objective
solution_paths['NUMBER_OF_VEHICLES'] = vehicle
stop = timeit.default_timer()
solution_paths['MODEL_RUN_TIME_MINUTES'] = (stop - start)*60
solution_paths.to_csv(r'general model solutions/{}_.csv'.format(str(vehicle)), index=False)
return 'ok'
q = queue.Queue()
def worker():
"""
Worker function to process vehicles from a queue (q).
"""
while True:
print("Start thread worker.")
vehicle = q.get()
print("Starting vehicle: {}".format(str(vehicle)))
run_single_depot_general_model(vehicle,
depots,
customers,
transportation_matrix,
vehicles,
bigm_input,
solver_time_limit_minutes_input)
print("Finishing vehicle: {}".format(str(vehicle)))
q.task_done()
print("End thread worker")
def create_and_process_queue(vehicle_range_list, max_num_threads):
"""
Creates a queue of vehicles to process. Creates threads to process the queue.
The number of threads are limited by max_num_threads.
"""
# add the vehicles to the queue
for vehicle in vehicle_range_list:
print("Adding vehicle {} to queue".format(str(vehicle)))
q.put(vehicle)
print("Create threads")
for i in range(max_num_threads):
time.sleep(10)
t = Thread(target=worker)
t.daemon = True
t.start()
q.join() # blocks until all queue items have been processed
min_vehicles = int(round(customers.DEMAND.sum()/60)+2)
max_vehicles = len(vehicles)+1
vehicle_range_list = []
for vehicle in range(min_vehicles, max_vehicles):
vehicle_range_list.append(vehicle)
vehicle_range_list.reverse()
create_and_process_queue(vehicle_range_list, 5)You can install cvrptw_optimization package to your conda environment using the following code.
pip install cimren-cvrptw-optimization
We ran the model for the total number of vehicles, , from 30 to 11. We set the maximum model run time to 480 minutes (8 hours). There is no solution for and since maximum model run time is reached.
Figure 2 illustrates routing, model objective, and run time minutes for each number of available vehicles set.
 |
|---|
| Figure 2: General model solution |
As we use less number of vehicles, total delivery hours is reduced by about an hour per vehicle removed.
Best solution is obtained when (Figure 3). Model run time is approximately 6 hours. Model objective is which is total drive hours.
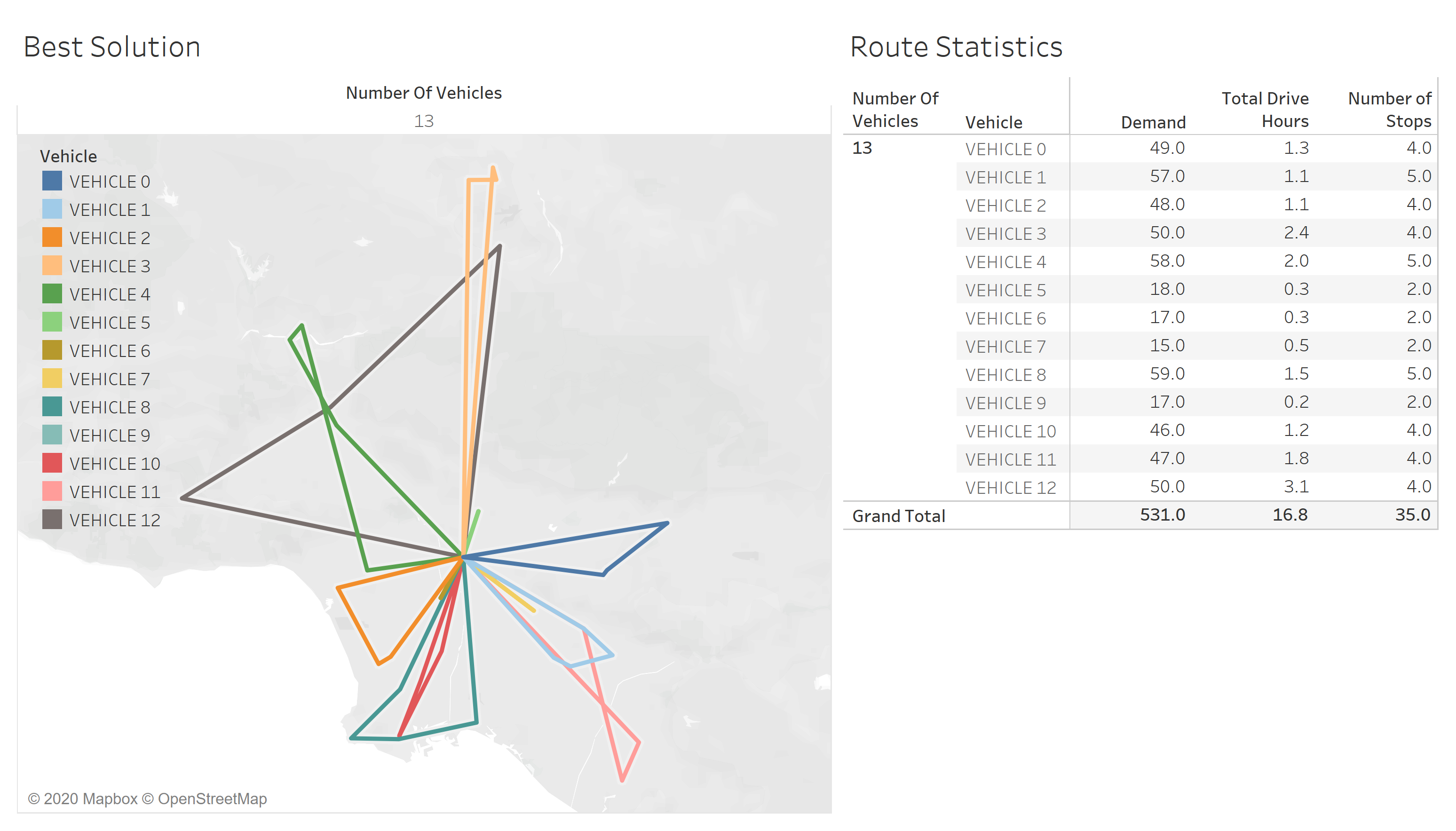 |
|---|
| Figure 3: Best general model solution |
We now implement column generation methodology.
Column Generation
We develop a column generation approach based on Dantzig-Wolfe decomposition. CVRPTW is decomposed into two problems, the master problem, and the subproblem to provide better bound when linear relaxation of the problem is solved.
The master problem considers only a subset of variables from the original while the subproblem identifies the new variables. The objective function of the subproblem considers the reduced cost of the new variables with respect to the current dual variables. The outline of branch-and-price algorithm is illustrated in Figure 4.
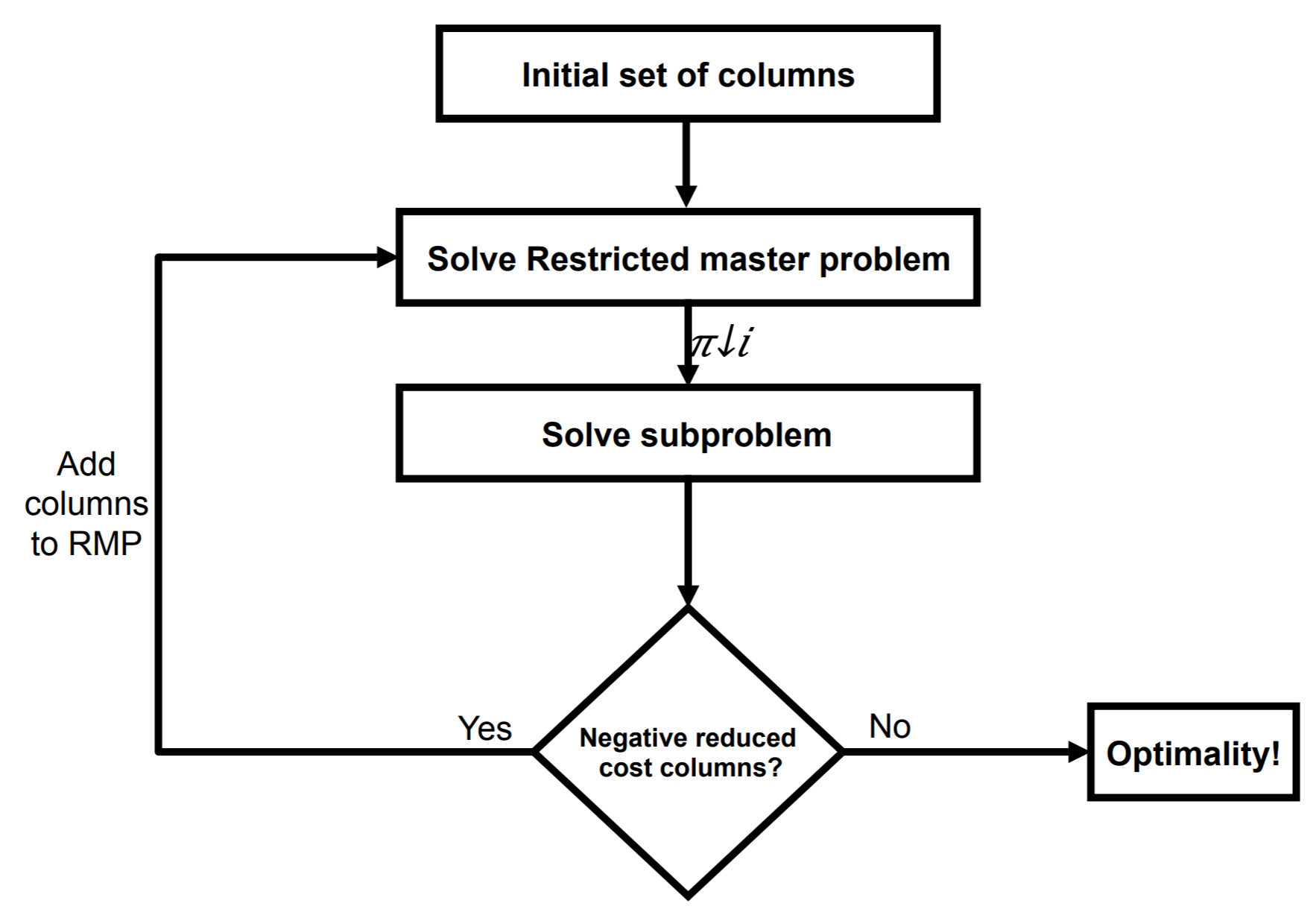 |
|---|
| Figure 4: Column generation algorithm |
In the column generation algorithm, the master problem is solved using an initial solution. It can be any feasible solution that meets all constraints. In this case, we start with the depot-store-depot routes. From this step, the dual prices of each constraint in the master problem are obtained. Then, the reduced cost is calculated and utilized in the objective function of the subproblem. After solving the subproblem, the variables (called columns in the master problem) with negative reduced cost must be identified. These variables are then added to the master problem and resolved iteratively. The process is repeated until the subproblem solution has only non-negative reduced costs columns. Theoretically, at that instance, the solution of the master problem is the optimal solution.
Master Problem
We consider all feasible single vehicle routes, , with respect to vehicle capacity that start and end at the same depot. Master problem selects sets of routes which minimizes total transportation cost.
Subproblem
The subproblem attempts to generate feasible routes with negative reduced costs to be added in the master problem. As the capacity of the vehicles, , is be the same for all vehicles, we solve the problem for . The explicit formulation of the subproblem is given as follows.
Column Generation Algorithm Implementation
We run the column generation in Python as follows.
import pandas as pd
from cvrptw_optimization import single_depot_column_generation_pulp as cg
# read input data
customers = pd.read_pickle(r'data/customers.pkl')
depots = pd.read_pickle(r'data/depots.pkl')
transportation_matrix= pd.read_pickle(r'data/transportation_matrix.pkl')
vehicles = pd.read_pickle(r'data/vehicles.pkl')
vehicle_capacity = 60
# run column generation
solution, iteration_statistics = cg.run_single_depot_column_generation(depots,
customers,
transportation_matrix,
vehicles,
vehicle_capacity,
mip_gap=0.001,
solver_time_limit_minutes=10,
enable_solution_messaging=0,
solver_type='PULP_CBC_CMD',
max_iteration=150) In the solution, we deliver with trucks driving total hours (Figure 5). Algorithm run time is less than 2 minutes.
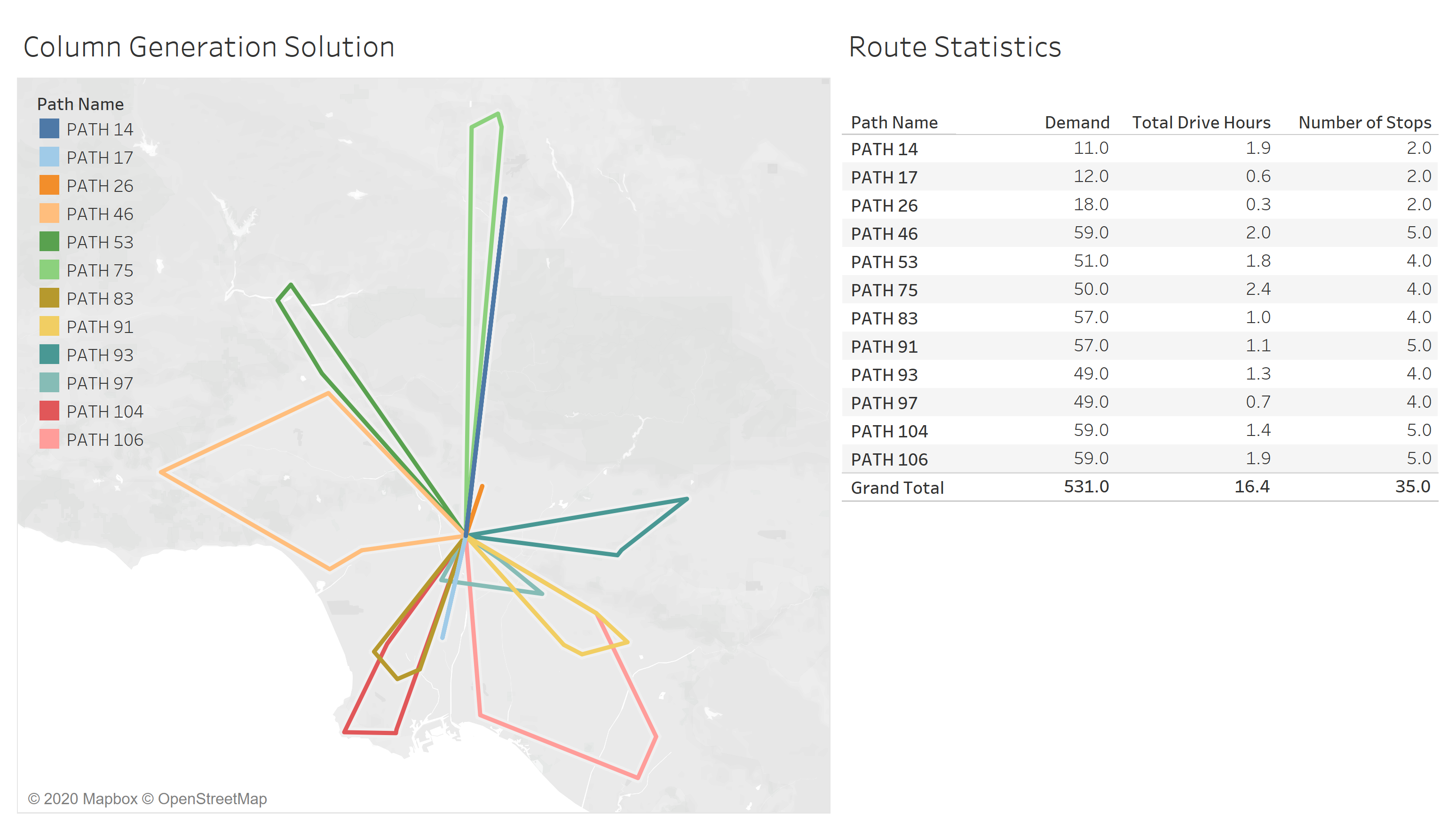 |
|---|
| Figure 5: Column generation solution |
Figure 6 shows algorithm convergence. Note that subproblem objective reached in iterations.
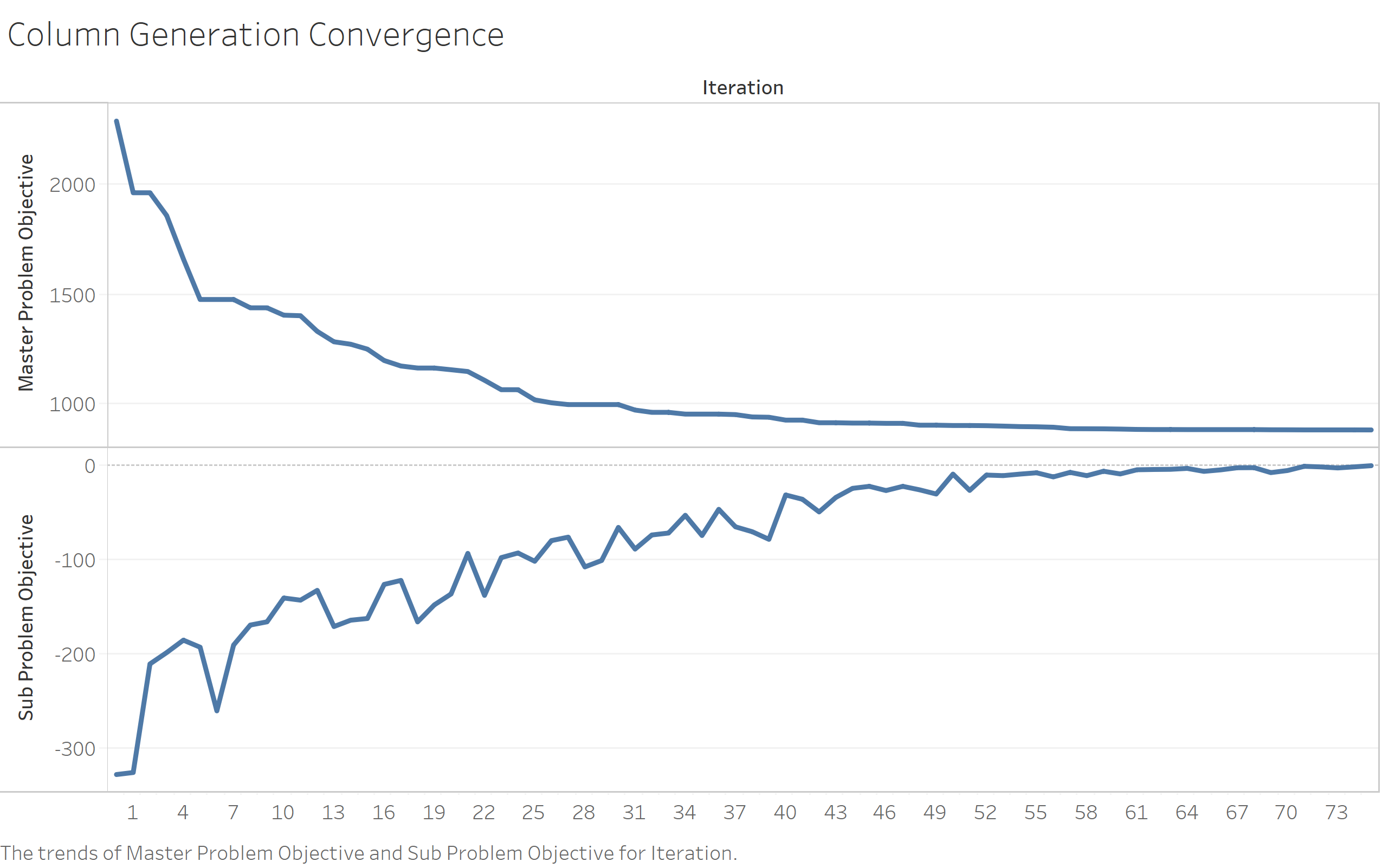 |
|---|
| Figure 6: Column generation algorithm convergence |
PPizza Solution
As a result, column generation uses less number of trucks than the general mixed integer formulation.
Figure 7 illustrates solution for PPizza with 12 trucks. Each truck leaves depot at 6am and returns by 5pm.
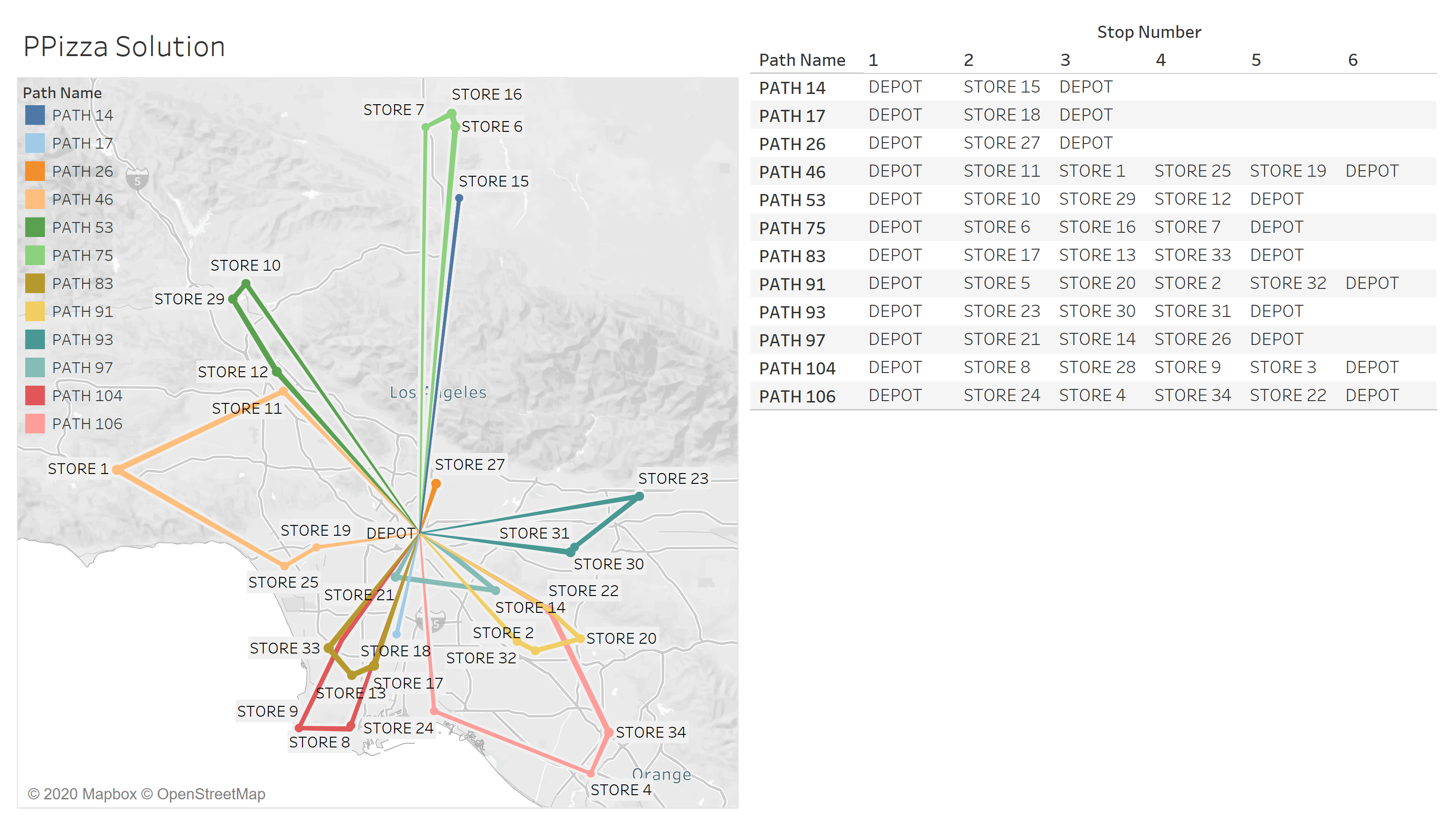 |
|---|
| Figure 7: PPizza solution |
References
Desrochers, M., Lenstra, J.K., Savelsbergh, M.W.P., Soumis, F. (1988). Vehicle routing with time windows: Optimization and approximation. In: Golden, B.L., Assad, A.A. (Eds.), Vehicle Routing: Methods and Studies. North-Holland, Amsterdam, pp. 65–84.







